（6）稳定系统

　　前面我们考察了系统的因果性，下面我们来看看系统的稳定性。在第一章里我们已经介绍过了系统稳定性的概念。系统的稳定性通常用“有界输入有界输出”原则（BIBO）来表达。若系统对任意的有界输入其零状态响应也是有界的，则称此系统为稳定系统。用数学表达式来说明就是：对所有的激励信号 e(t)，若|e(t)| <= Me，则其响应r(t)满足|r(t)|<=Mr，则称该系统是稳定的。式中，Me,Mr为有界正值。

　　和前面讨论因果性一样，下面我们还是从系统的单位冲激响应特性来考察它与系统的稳定性的关系。

　　一个离散的线性时不变系统是稳定系统的充要条件是系统的单位冲激响应绝对可和，即：

　　证明：(1)充分条件：

　　　　　设 ，则如果输入是有界的，即对于所有n皆有 ，则

　　　　　即输出有界，故原条件是充分条件。

　　　(2)必要条件：利用反证法。已知系统稳定，假设

　　　我们可以找到一个有界的输入

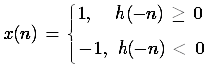
　　　则

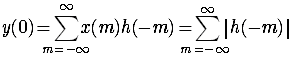
　　　即输出无界，这不符合稳定的条件，因而假设不成立。所以 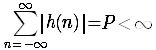又是稳定的必要条件。

　　　根据上面所给的结论，我们根据系统的单位冲激响应可以确定是否稳定。稳定性是系统的一个很重要的指标。因为系统如果不是稳定的话，则系统在激励的作用下，产生的输出将是不可预料的。显然，这样的系统是无法应用于实际的信号处理的。因此，研究系统在何种条件下满足稳定性的要求，就具有很重要的意义。后面，我们还要从系统的传递函数出发来研究系统的稳定性。