序列x(n)的DTFT频谱 是连续的（当然，同时它也是周期的），而DFT所求的是这个连续谱上的均匀抽样。如果用X(k)去近似 ，就一定意义上来讲，就好象是在栅栏的一边通过栅栏的缝隙(对应离散点)去观看另一边的景象(对应连续频谱)，只能在离散点的地方看到真实的景象，因此，那些被栅栏挡住的（频谱）部分是看不到的，这就有可能漏掉一些较大频率分量。我们称这种现象为"栅栏效应"。
　　当然，在实际问题中，"大的频谱分量"被挡住的情形还是很少的，栅栏效应并不是一个很严重的问题。尽管如此，我们还是有必要讨论清楚如何避免或者说减少这种栅栏效应。
　　那么，到底怎么才能减少这种栅栏效应呢？
　　知道了栅栏产生原因，我们才能采取有针对性的方法来减少它。从根本上讲，用离散的DFT谱来近似连续的DTFT谱，误差总是有的，即从理论上，栅栏效应是不可能消除的。不过，也正是因为DFT离散谱是DTFT连续谱的抽样，为了提高近似程度----也即减少栅栏效应，我们可以在DTFT连续谱上多抽取些频率样本。这样，谱线变密了，那些原先看不到的频谱分量，就有可能看到了。
　　那么，怎样才能实现在DTFT连续谱上抽取更多的频率点呢？按照本章前面给出的DFT与DTFT的关系 ，只要增加下列DFT的计算式中的N值即可

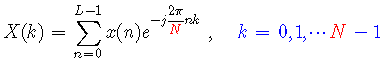
　　考虑到增加N值，会使得L<N，即频率点数大于序列的长度，按照前面我们所讨论的，可以在序列后面补上一些零值，这并不改变DFT结果。因此，减小栅栏效应的具体方法是：在所取数据的末端增加一些零值点，同时保持原有数据不改变。