现在，DFT的应用已遍及各个科学技术领域，本节将对DFT应用过程中的几个问题进行深入探讨。

5.9.1频带分析宽度与频率分辨率

　　通常，在对连续时间信号进行抽样前，已经滤除了信号中一定频率f_h以上的频率分量，即这时信号的最高频率为f_h。
　　如果设抽样频率为f_s，则按照抽样定理的要求，为了不产生频谱混叠，采样频率必须至少是信号最高频率的两倍，即

　　因此，信号的抽样间隔为

　　于是

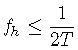
　　这是抽样时间间隔与信号所含的最高频率之间的关系。
　　由DFT的定义可知，DFT计算得到是离散的频谱，设频率之间的间隔为F，它是DFT的频率分辨率，则序列的数据长度Tp与它满足

　　由于 ，所以 ，于是有 ，即 。因此，若序列样本点数N是给定的（固定了），则DFT的频率分辨率F与原信号的最高频率f_h之间是矛盾的。也就是说，当增加f_h（即能分析的信号带宽增加了）时，则F必须增加，而这将导致DFT的频率分辨率下降；反之，如果提高频率分辨率（即减小F，减小频率分量的间隔），则f_h必须降低，也就是能分析的信号带宽降低了。
　　换言之，要想在保持F或f_h不变的同时，还能提高另外一个的性能（对频带来讲，就是越宽；对频率分辨率来讲，就是越高），就必须增加序列的数据长度，这就是 说明的道理。