显然，如果直接按照上面的原理来设计程序，最为直观的办法是利用程序设计语言的递归来实现。不过这种实现方法中由于要不断地进行函数递归调用，所以效率会受到一定的影响。尽管如此，由于这种实现方法所编写的程序，与FFT的原理（公式）是完全一一对应的，所以非常容易书写、调试和理解（阅读）。我们把这种用递归来编写FFT算法留给大家作一个小练习吧。
　　那么能不能避免递归调用呢？答案是肯定的。为了说明说明如何不用递归的方法来实现FFT，下面我们以N=8的FFT为例，来进行说明。
　　按照FFT的原理，我们下面逐步分析计算过程：
　　（1）要用计算 8点
　　　　　[ x(0), x(1), x(2), x(3), x(4), x(5), x(6), x(7) ]
　　　　对应的 DFT
　　　　　[ X(0), X(1), X(2), X(3), X(4), X(5), X(6), X(7) ]
　　　　可以先分别计算两个4点
　　　　　[ x(0), x(2), x(4), x(6) ] 和 [ x(1), x(3), x(5), x(7) ]
　　　　对应的DFT
　　　　　[ X(0), X(2), X(4), X(6) ] 和 [ X(1), X(3), X(5), X(7) ]
　　　　然后两组DFT结果分别交叉相加减，即得8点DFT。
　　（2）而4点子序列 [x(0), x(2), x(4), x(6) ]所对应的DFT，又可由两组2点序列
　　　　　[ x(0), x(4) ] 和 [ x(2), x(6) ]
　　　　对应的DFT来求出（通过交叉相加减）。
　　　　同理，[ x(1), x(3), x(5), x(7) ] 的4点DFT也是如此，可以由两组2点序列
　　　　　[ x(1), x(5) ] 和 [ x(3), x(7) ]
　　　　对应的DFT来求出（通过交叉相加减）。
　　（3）而2点子序列
　　　　　[ x(0), x(4) ]、[ x(2), x(6) ]、[ x(1), x(5) ]、[ x(3), x(7) ]
　　　　对应的DFT可以分别用下面1点序列的DFT来求出：
　　　　　[ x(0) ]、[ x(4) ]、[ x(2) ]、[ x(6) ]、[ x(1) ]、[ x(5) ]、[ x(3) ]、[ x(7) ]
　　　　根据DFT的定义，1点序列的DFT就是它们自身。

　　上面的这个分析过程可以用下面的图示来说明：

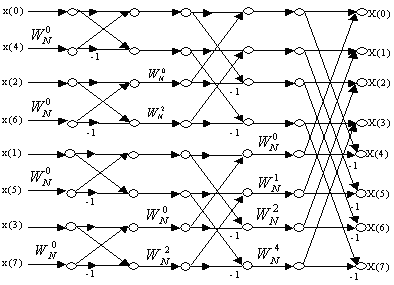
图5-2 N=8时的FFT流程图