上式表明：X(k)可以用两个N/2点的DFT G(k)和H(K)重建出来。其中含有N次乘法 。不过，利用G(k)和H(k)的周期性，我们可以把这N次乘法减少一半（N/2次）。

　　真的？那，怎么做呢？

　　具体的做法是：将范围 分成两部分，即

与

　　于是，关于X(k)的N个等式就可以写成下面的两组N/2个等式：

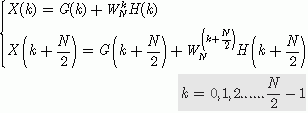
　　啊！ 看起来好象更复杂了。不过，对上面这个计算式子，我们可以进一步简化。

　　我们注意到G(k)与H(k)实际上是周期的，它们的周期为N/2，因此
　　G(k+N/2)=G(k)，H(k+N/2)=H(k)
　　由旋转因子的性质，我们不难得到

　　于是

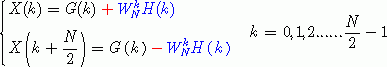
　　显然，上面的这种奇偶分解过程可以不断进行下去，分解到最后，运算就成了两个原序列值进行加减运算了---因为这个时候N=2，而旋转因子的指数为零所以等于1。通过这种分解，DFT的总的运算量就减少了很多。对此，我们可以进行一下简单的分析。
　　当N是2的M次幂时，上面所说的分解要进行M级，其中每级都会包含N/2次乘法，N次加减法，因此快速算法的全部运算工作量为：
　　复数乘法共 次
　　复数加（减）法共 次
　　而直接用DFT定义来计算，复数乘法与复数加（减）法的次数分别是N²和N(N-1)次。

　　后面我们将从程序设计的角度出发，来考虑如何编程实现上面的快速算法，即讨论快速傅里叶变换的算法实现流程。