对序列x(n)，（n=0,1,2……,N-1）求它的N点DFT，假定N是2的整数次幂，即 ，其中M是正整数。把x(n)按下标n的奇偶性分成两组，根据DFT的线性特性，可以将原序列的DFT可以写成这两组子序列的DFT的和，即

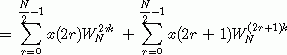
　　上式中x(2r)是序列x(n)的偶下标部分，而x(2r+1)则是序列的奇下标部分，r的取值范围是0,1,…N/2-1。上式可以进一步写为

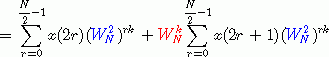
　　由于

　　因此，上面求和式可以改写成

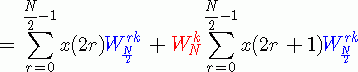
　　根据DFT的定义式，上面的和式实际上是两个N/2点的序列的N/2点DFT！

　　看出来了这一点吗？不要被序列x(2r)的下标迷惑住了。上面式中的和式不正是N/2个序列值与N/2个相应的旋转因子相乘吗？注意旋转因子的点数也是N/2！我们换个角度来看DFT的定义式，就可以理解上面的和式为什么是两个N/2点序列的DFT了。