我们已经知道，对于有限长序列，它在频域也可离散化成有限长序列，即进行离散傅里叶变换。而在在数字信号处理（如滤波器设计）、信号的频谱分析（如在通信、图像传输、雷达、声纳等中的频谱分析）、系统的分析和设计实现等方面，都会大量用到DFT计算。然而，在相当长的时间里DFT并没有得到广泛的应用，这是为什么呢？
　　主要的原因是因为直接按定义计算DFT的计算量太大了，实在不无法满足实际应用的需求。直到快速傅里叶变换算法FFT出现，这种状况才得以改观。FFT这种快速算法极大地减少了计算DFT的运算量，并且它在硬件（如专用的数字信号处理芯片）上实现也非常容易，这才使得基于DFT的信号分析飞速发展起来。
　　本节将从DFT的算法复杂度入手，详细讨论FFT算法的原理与实现流程。

5.8.1 DFT的算法复杂度

　　根据DFT与IDFT的定义，它们二者的差别只在于W_N的指数符号不同（是互为共轭的），以及一个常数乘因子 ，因此IDFT与DFT的运算量是完全相同的，下面我们只讨论DFT正变换式的运算量。
　　通常，x(n)和  都是复数，算得的X(k)也是复数，因此每计算一个X(k)值，都需要N次复数乘法（x(n)与 相乘）以及（N-1）次复数加法。而序列X(k)一共有N个点（k从0取到N-1），所以要完成整个DFT运算总共需要N²次复数乘法及N(N-1)次复数加法。
　　由于复数运算实际上是由实数运算来完成的，我们可以把DFT式改写成

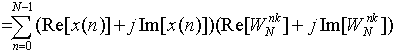
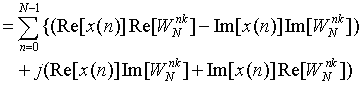
　　由上面的式子可知，一次复数乘法需要四次实数乘法和二次实数加法；一次复数加法则需二次实数加法。这样一来，每算得一个X(k)就需要4N次复数乘法及2N+2(N-1)=2(2N-1)次实数加法。所以整个DFT运算总共需要4N²次实数乘法和2N(2N-1)次实数加法。

　　真的要这么多的运算量吗？是不是还可以简化一下？比如说有些旋转因子等于1的时候，不是就不用乘了吗？