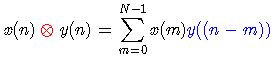解铃还需系铃人。要求解卷积的回绕，我们可以试试直接从等于的右端入手，利用IDFT的定义来求解等式左边的值。即：

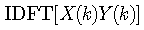
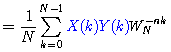
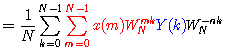
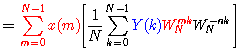
（这一步是关键！）

　　根据IDFT性质，上式中对 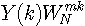求IDFT所得到的应是y(n)的时移序列的回绕。即

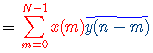
　　而这正是序列x(m)与 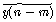的卷积运算！由于序列 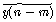是序列y(m)反褶、移位后再作回绕所得的信号，因此这种“卷积”运算对于序列x(m)和y(m)来讲，并不是传统意义下的卷积了（因为运算过程中多了一个“回绕”的操作）。

　　如果我们要求序列下标的有效范围仍是从0到N，则上面的这种对序列的时移后再回绕的操作，可以通过在圆周上进行移位来一步完成。而根据DFT时移特性中所介绍的圆移的概念，我们的确可以如此。所以，我们可以把上面式子改写成圆移的形式，即

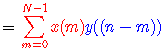
　　这样，如果我们把传统卷积过程中所包含的“平移”操作改为“圆移”，即相当于同时完成“平移”和“回绕”操作，则上面的这种对序列x(m)和y(m)而言是特殊的“卷积”运算，仍旧与传统的卷积运算一样，包含了“反褶”、“移位”、“乘积”与“求和”等步骤。（只不过这时的“移位”实际上是圆周上的移位。

　　既是为了突出这两种卷积之间的不同之处，也是为了突出它们之间的相同处，我们可以称过去定义的卷积为“线卷积”，而定义这里新引入的特殊形式的卷积为“圆卷积”，同时引入一个新的卷积符号来表示这种运算，即两序列之间的圆卷积定义如下：