(6)奇偶虚实特性
参照连续时间傅里叶变换,可以证明DFT的奇偶虚实性。这只要利用欧拉公式,将DFT变换式中的复指数改写成实部与虚部的形式,则很容易证明有下列结论成立:
(a)对奇对称和偶对称的序列
奇函数的DFT是奇函数;
偶函数的DFT是偶函数。
(b)对实序列:
实偶函数的DFT是实偶函数;实奇函数的DFT是虚奇函数。
实函数的DFT,其实部是偶函数,虚部是奇函数;其模是偶函数,而相位是奇函数。
(c)对虚序列:
虚偶函数的DFT是虚偶函数;虚奇函数的DFT是实奇函数。
虚函数的DFT,其实部是奇函数,虚部是偶函数;其模是偶函数,而相位是奇函数。
时域卷积是一个很常见的运算,这一方面是因为线性时不变的特性 ,另一方面是因为对频谱进行滤波处理时,要在频域进行乘法,从而导致信号(序列)在时域发生卷积。例如,对于连续时间傅里叶变换,以及本章前面讨论的离散时间傅里叶变换DTFT,都具有这样的性质。同样的,对于离散傅里叶变换DFT,也具有类似的特性。
序列x(n)与y(n)的卷积满足下面的关系:
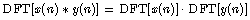
即两个序列卷积的DFT等于各序列DFT的乘积。我们可以发现,对于DFT来讲,卷积定理的也是满足的,并且与连续时间傅里叶变换、离散时间傅里叶变换是相一致的。
(不过,我想大家可能有一个疑问,为什么在有些参考书中,对于DFT中的卷积定理是另外一种解释呢?不用奇怪,下面我们就来更深入的讨论一下这个问题,以便加深大家对DFT理解。)
如果将本性质换一种形式表达,改写成逆变换的形式,则有
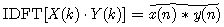
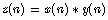 ,根据DTFT的卷积定理得
,根据DTFT的卷积定理得

于是,

根据DFT与DTFT的关系,得

即
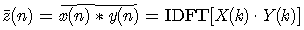
现在问题是:如何方便地求解序列卷积的回绕呢?或者说,这种形式的运算与普通的卷积有什么关系呢?