（3）频移特性

　　如果序列的DFT频谱在频域发生平移，与结果将导致序列在时域发生一定的改变。

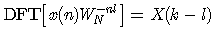
　　这个定理表明，如果序列在时域乘以指数项W^-nl，则离散傅里叶变换就向右圆移m单位。这可以看作是调制信号的频谱搬移，也称调制定理。

　　这个定理的证明比较容易，可以直接按照DFT的定义来证明。即

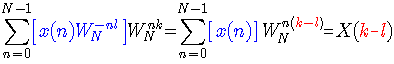
　　DFT的对称性与连续时间傅里叶变换的对称性非常类似 [请在此加上超级链接，指向第二章中傅里叶变换的性质一节里的对称性部分 ]，即如果将某序列的DFT变换结果，当作一个新的时域序列进行DFT，所得的频谱与原序列有如下的关系存在

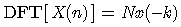
　　上面的公式表明，当对离散谱再次进行DFT运算时，得到的结果是原时域序列反褶的N倍。显然，如果原序列具有偶对称性，则其DFT结果就是原时域序列的N倍了。

　　证明：由IDFT的定义

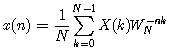
　　可得

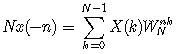
　　对上式进行变量替换，n->k得

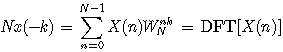
　　当时域序列取反褶、取共轭或同时取反褶和共轭时，其DFT频域序列的变化规律如下：

　　序列反褶，对应频域也反褶：

　　序列共轭，频域共轭加反褶：

　　序列反褶加共轭，频域共轭：

　　这些特性如下表所示。

表5-2 DFT的反褶和共轭特性

　　上面这些性质可以直接利用DFT的定义，结合复数关于共轭的性质即可得到证明。这里就不详细说明了。请读者自己动手证得试一试。