由于DFT实际上是对DTFT在频域的一种抽样，所以DFT的性质与DTFT的性质有着很多相似之处，大家在学习的时候，要注意进行对比。另外，也正是因为DFT只是DTFT的抽样，所以它也有一些比较特殊的地方---即与其它傅里叶分析方法不同的地方。对于这些地方，大家一定要从DFT的定义出发，找出这些特殊性的本质原因所在。千万不要被它们的表面现象所迷惑住了。当然，我们会在这些特殊的地方作比较详细的讨论的。至于其它一些相似的地方，我们会比较简要的进行说明，甚至留给大家自己去试着证明一下。

　　若

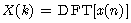
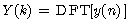
　　则

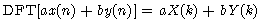
　　式中a,b为任意常数。

　　如果序列x(n)发生时移，变成x(n-m)，则新序列与原序列的DFT频谱之间的关系如何？下面我们从多个方面（角度）来进行讨论。

　　首先，根据DFT与DTFT的关系—即序列DFT是序列DTFT的抽样，我们对移位后的序列x(n-m)，先求它的DTFT，得下面的关系式

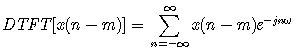
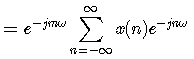
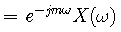
　　然后在此基础上对频谱进行抽样，即可求得序列的DFT如下

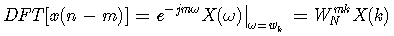
　　这就是序列DFT的位移特性。显然，由于上式中 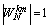，因此序列的时移不会影响DFT频谱的幅度。