在总体上讲，通过DFT所得的频谱，（1）它是离散的－－这是显然的，因为DFT对DTFT连续谱的抽样；（2）它也是周期的（关于下标k）－－这是DTFT频谱的周期性的体现（DTFT是抽样信号的傅里叶变换，时域抽样所以频域周期）。

　　（1）周期性：

　　序列的N点的DFT离散谱关于下标k是周期的，周期为N，即

　　利用DTFT的周期为

　　证明如下：

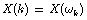
　　而

　　所以

　　由于DTFT的周期是 ，即

　　因此

　　（2）实序列频谱的共轭对称性

　　若 是实序列，其N点DFT关于原点和N/2都具有共轭对称性，即

　　关于原点共轭对称：

 或

　　关于N/2点共轭对称(N为偶数)：

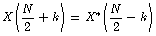 或

　　在上面的公式中，只要证明了第一个公式，其余的都可利用DFT频谱的周期性证明。

　　证明：

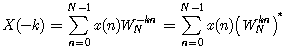
　　根据“乘积的共轭等于共轭的乘积”，并且“实数的共轭还是它自身”，可得

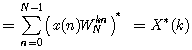
　　有了这些共轭特性，我们很容易得到一个推论：

　　实序列的DFT频谱关于原点和N/2点是幅度对称的。