（2）当L＞N时

　　设序列为x(n)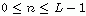， 。我们定义序列x(n)关于N的回绕序列为

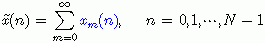
　　其中

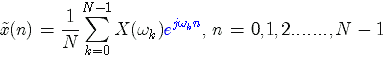
　　显然，当L＝N时， 。

　　可以证明，x(n)与 的DFT结果是相等的，如果用DFT的矩阵形式，就是

　　证明：将矩阵 (N×L)中每N列分出一个N×N的子阵。第m个子阵中的元素为

　　由旋转因子的特性，不难得 ，于是

　　所以

　　于是

证毕.

　　根据上面证明的结论，我们不难推出：任意两个序列，只要它们的回绕序列是相等的，那么它们的DFT结果也就是相等的。因此，多个完全不同的序列，可以对应完全相同的DFT结果！换句话说，也就是一个DFT结果实际上对应着多个序列！

　　另外，我们还可以发现，利用回绕这种手段，可以减少DFT的运算量。有兴趣的读者可以自己试着进行说明。

　　经过上面（1）和（2）的讨论，我们知道，如果序列的长度L小于DFT点数N，可以通过补零使它们相等，并且这不会影响DFT结果；而当序列长度L大于DFT点数N时，单个DFT结果会对应多个时域信号。这就是说：序列短了（L<N）可以补一样长而不影响DFT结果；序列长了（L>N）会发生多个序列对应同一个DFT结果，运算就不是可逆的了。