有时，我们要考察信号在某段频率范围上的频谱变化情况。由于实际限制，只能保存该频段范围中的有限个频率点的频谱密度值，通常这些点在该频段范围中是均匀分布的。(也可以视为是对该频段进行频域抽样。)
　　设有频率范围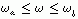 ，如何求在这个范围上均匀分布的N个频率的DTFT呢？

　　首先，我们要确定这些均匀分布的频率点的具体频率值，然后我们就可以利用前一节的算法，求出它们的频谱密度值来。显然，这些均匀分布的频率之间的间隔为

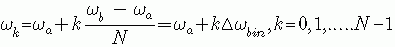
　　其中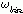 表示N个频率点的间距，它可以用下面的公式算出：

或

　　根据前面所讨论的算法，可以用下面的算法解决上述问题。

#include <comlx.h>
complex dtft();
void dtftr(int L, double * x, int N, complex * X, double wa, double wb)
{
　　int k;
　　double dw = (wb-wa)/N;
　　for (k=0; k<N; k++)
　　X[k] = dtft(L, x, wa+k*dw);
}

　　很多情况下，我们要研究DTFT的一个周期区间范围---即整个奈奎斯特区间范围---中均匀分布的N个频率点的频谱密度值。虽然我们依然可以用上面给出的通用算法来计算这些频率密度值，但由于这种情况的特殊性（因为频率区间是整个奈奎斯特区间！），我们可以引入一种新的变换----离散傅里叶变换DFT----来更直接、更方便地解决这个问题。有了DFT，对于在DTFT的一个频谱周期内均匀分布的N个频率点处的频谱值，我们可以用离散时域序列直接求解计算。我们将从下一节开始详细讨论这个问题。