在本节，我们将重点考察DTFT的计算方面的问题。与前面一样，序列的长度是有限的。我们关心的重点是如何计算其频谱中某些频率处的频谱密度值。这是因为要对信号进行数字处理，并保存频谱分析的结果，必须解决如何求解频谱中各频率点的频谱密度的问题。

5.5.1 某个频率处的DTFT频谱密度值

设x(n), n=0,1,2……,L-1是已加窗的信号，其频谱为

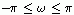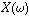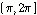　　根据上面的公式，对于 中的任意值都可以计算出 来。利用抽样信号频谱的周期性，可以把区间 映射到 ,于是得到新的区间 。

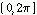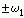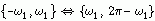　　例如 的频率分量在 处，于是 。因此，

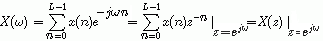
　　即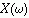 是多项式X(z)在 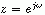处的抽样。这样，我们的注意力转向如何求下列多项式的值。
　　对下面的多项式，

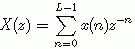
　　我们可以利用Horner算法来多项式的值。其算法伪代码为：
　　对每个给定的复数z，执行下面的操作
　　

　　　　X=0
　　　　For n=L-1 down to n=0 do:
　　　　　　X = Xn + z-1X
　　当循环结束时，X即为多项式X(z)的值。
　　下面是具体的代码实现。

#include <comlx.h>
complex dtft(int L, double* x, double W)
{
　　complex z, X;
　　int n;
　　z = cexp(cmplx(0,-W))
　　X = cmplx(0,0)
　　for (n=L-1;n>=0;n--)
　　X = cadd(cmplx(x[n],0),cmul(z,X));
　　return X;
}
关于程序的说明：在上面的代码中，函数cexp(A)求复数A的指数，函数cadd(A,B)求复数A和B的和，函数cmul(A,B)求复数A和B的乘积。