5.3.4 DTFT的基本性质

　　DTFT实际上是对抽样信号(离散时间序列)的傅里叶变换，因此具有与连续时间傅里叶变换非常相似的性质，只不过表现形式略有差异。因此，下面只简要列出这些性质，并不作详细的证明。有感兴趣的读者可以利用连续时间傅里叶变换的性质，特别是抽样信号的频谱特点来证明它们。为表述方便，设序列x(n)的DTFT为 。

　　(1) 周期性：

　　　　显然，这种周期性是因为序列x(n)是某连续信号的均匀抽样，因而其频谱是按抽样频率f_s周期重复的。根据抽样定理，频谱重复区间的宽度为f_s，称区间[-f_s/2, f_s/2]为奈奎斯特区间，在数字频率意义下，奈奎斯特区间为 ，为研究方便，通常使用 作为奈奎斯特区间。
　　(2) 线性：

，a_k为常数。

　　(3) 平移：
　　　　　　时移特性：
　　　　　　频移特性：
　　(4) 反褶、共轭：
　　　　　　反褶：
　　　　　　共轭：
　　(5) 时域扩展
　　　　　　序列的时域扩展定义如下：

　　　　　　它的DTFT为

　　(6) 频域微分(时域线性加权)

　　(7) 卷积定理

　　　　　　　　设

　　　　时域卷积：

　　　　频域卷积：

　　(8) 帕斯瓦尔定理

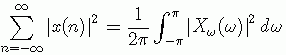
　　　　这个定理也被称为能量定理。它说明：序列的总能量等于其傅里叶变换模平方在一个周期内积分取平均，即时域能量等于频域一周期内总能量。