5.3.3 频率归一的DTFT

　　用抽样序列的DTFT所得的频谱，是一个以抽样频率f_s为周期的周期频谱。为了研究方便，我们对这个周期频谱进行频率归一化，用归一频率 作为新的频率变量，于是

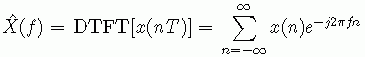
如果用角频率来表示就是

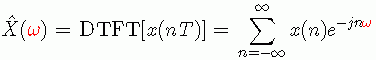
通常上面这种表示形式用得更多一些，在今后的讨论中，更多是这种角频率的形式。
　　用归一化频谱求时域序列的逆变换的公式如下：

　　这样一来，我们就不必再关心信号的抽样间隔，而只需将得到的信号抽样值顺次保存起来，再作变换即可，从而大大方便了抽样信号在计算机等数字处理设备上的分析处理。因此，今后，在不致引起混淆的情况下，我们用x(n)来代表x(nT)。
　　为了与信号的实际物理频率区别开，我们称归一化处理后的"频率"为数字频率，单位为弧度/样本（对应数字角频率）或赫兹/样本（对应数字频率）。
有些参考书也称数字频率为归一化频率。
　　对于这种频率归一化，大家可以这么理解：
　　　（1） 既然对于序列而言，元素间的时间间隔Ts并非必须的，那么将其视为1也就不会带来什么问题，即不会影响序列的存储。
　　　（2） 对于序列对应的连续频谱，都是周期的，这个周期由信号的采样频率完全决定。而信号的采样频率是可以变化的，也就是可以按照实际需要给出。换言之，连续谱的周期并不是一个特别重要的限制条件。
　　　（3） 对于周期谱，我们通常只需（也只能如此）关心和存储一个周期的内容，因此，至关重要的是一个周期内各频率对应的频谱密度值的相对关系，而周期的具体大小并不会影响这一点。
　　因此，我们把频谱的周期统一归整为1---即将实际物理频率改为对采样频率的相对频率（数字频率），这种做法是可行的。当然，在必要的时候，要恢复（求解）数字频率所对应的实际物理频率也是非常容易的。