5.3.2 关于DTFT公式的几点说明：
　　（1） 从公式可知，抽样信号的频谱 仅从抽样值x(nT)即可算出。
　　（2） 是f的周期函数，周期为f_s。即

　　　　这一点也可以根据式中 的周期性导出。因此，在进行频谱分析的时候，可以只关心奈奎斯特频率区间[-f_s/2，f_s/2]。
　　（3） 如何求DTFT的逆变换？如果将DTFT的计算式视为周期函数 的傅里叶级数展开，则抽样值x(nT)就是相应的展开系数，因此，这些展开系数x(nT)就可以用IFS公式从 重建出来：

　　　　这就是DTFT的逆变换公式。
　　（4） 数值近似问题。上式不仅仅是一个求解抽样信号频谱的计算公式，其实也可以看作是对模拟信号x(t)的频谱的一种数值近似！这个频谱的近似计算方法，也可以从纯数学的角度来得到。即：对于模拟信号x(t)的傅里叶频谱计算公式，根据积分的定义，可以近似为:

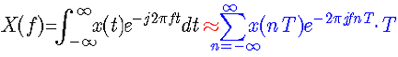
　　　　　也即

　　　　　在T->0时，上面的式子在极限意义下是精确相等的，即

　　（5） 工程近似问题。在实际计算信号的频谱时，还有两个工程近似的问题需要解决。
　　　（a）在时域，只能保留x(nT)有限数目的值，如L个样本，n=0,1……L-1。所以要用截断求和来近似上式：

　　　　　 这种近似需要在时域加窗，随之而来的是混叠和泄漏。后面我们再就此进行详细的讨论。
　　　（b）在频域，也只能保留有限的频谱值，即只在一些离散的频率处对 取样，用有限的离散值来近似原来的周期连续频谱。这就是我们后面要详细讨论的离散傅里叶变换DFT。
　　（6） Z变换。从上式可以导出Z变换与DTFT的关系。令 ，则