为了将信号输入计算机进行实际处理，信号需要被离散化，这就要对信号进行抽样。根据抽样定理 ，抽样率fs必须足够大，才能避免发生频谱混叠，或使频谱混叠尽可能的小。必要的时候，还应该在抽样之前对信号进行防混叠的模拟预滤波处理，将信号的频谱限制在一定的范围内，以满足抽样定理的要求。

　　计算机只能处理离散的有限数据，所以，对于连续时间信号，我们要做的第一件事情，就是要把它离散化，用离散信号的频谱来分析研究连续信号的频谱，因此，可以认为是对连续信号频谱的一次近似。这是第一次近似。（啊？那言外之意是还有好几次？当然！）

　　设连续时间信号x(t)的频谱函数为X(f)，对信号按时间间隔T抽样，得如下抽样信号：

　　利用每二章学过的知识，对上面的信号进行傅里叶变换，得

　　即：信号时域抽样（离散化），将使得频谱周期重复，抽样信号的频谱 等于原连续时间信号的频谱倍乘fs后周期重复。

　　要指出说明的是：上面的这个结果（结论）并没有要求抽样过程必须满足抽样定理的要求。也就是说，信号不必是频带受限的，抽样频率也可以任意选取。

　　那要是满足抽样定理的要求，会有什么好处吗？

　　如果抽样频率满足抽样定理的要求，则在奈奎斯特区间中，抽样信号的频谱 与原模拟信号的频谱X(f)满足下列关系式

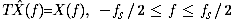
　　反之，如果抽样频率不满足抽样定理的要求，信号的频谱发生混叠，则可以认为是其它范围中的X(f)"延伸"过来了，即

　　因此，在奈奎斯特区间内，模拟信号的频谱可以（1）当满足抽样定理时，用抽样信号的频谱来还原；（2）若不满足抽样定理，则用抽样信号的频谱来近似。