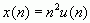4.6.2 幂级数展开法

　　根据Z变换的定义，序列x(n)的z变换实际上可以视为 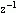的幂级数，即

从这个定义式来看，序列的取值用作了对应幂次项的系数。反过来说就是，把相应的幂次项“收集”起来，就组成了Z变换对应的序列。这就是所谓幂级数展开法的基本思想。

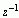　　因此，只要在给定的收敛域内，利用某些方法（比如说多项式的长除法---对多项式进行除法的过程与对数的除法是相似的，下面我们将看到这一点。），将变换式 按 展开成幂级数的形式，则所有幂级数的系数所对应的序列就是X(z)的原序列 。

　　一般情况下，X(z)是一个有理函数，令分子多项式为N(z)，分母多项式为D(z)。如果X(z)的收敛域是|z|>R₁，即x(n)是因果序列，则N(z)和D(z)要按照z的降幂（或z^-1的升幂）次序进行排列。如果收敛域是|z|<R₂，即x(n)是左边序列，则N(z)和D(z)要按照z的升幂（或z^-1的降幂）次序进行排列。

　　下面我们来看一个例子，体会一下如何用长除法求逆Z变换。

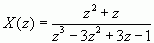　　例：求收敛域分别为|z|>1和|z|<1时， 的逆变换x(n) 。

　　解：（1）当|z|>1时

　　根据ROC性质，由于X(z)的收敛域是|z|>1，所以序列 是因果序列，此时X(z)按照z的降幂表示成

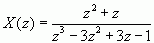
　　进行长除

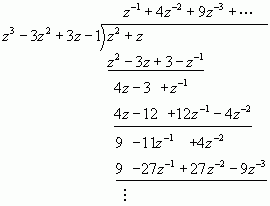
　　所以

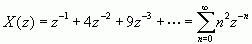
　　从而