如果给定了z变换X(z)，要求它所对应的序列x(n)，则称为逆z变换，表示为 求逆Z变换的方法主要有三种：
　　（1）将X(z)函数式用部分分式展开，求出逐项的逆变换，最后求和；
　　（2）还可以借助于长除法将X(z)展开幂级数得到x(n)。
　　（3）围线积分法（也称留数法）。其中，部分分式展开法比较简单，因此应用最多，而对于另外两种计算方法应用则较少。本节主要介绍前两种方法。

4.6.1 部分分式展开法

　　部分分式展开法基本思路是：把 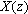展开成一些简单常见的部分分式之和，然后分别求各部分分式的逆变换，最后把各逆变换相加即可得到 。

　　产生上述思想的原因在于序列的Z变换 通常是变量z的有理函数，可以表示成有理分式的形式，如下式所示：

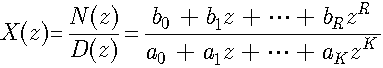
　　这样，就可以通过将它分解成为一些较简单的小分式的和，利用简单小分式的逆Z变换易于求得的特点，来实现对原变换式的逆Z变换的求解。

　　在拉氏变换一章中我们已经讲述了用部分分式展开法求拉氏逆变换。逆z变换的部分分式展开法与拉氏逆变换类似。

　　在进行部分分式展开时，为了方便起见，通常是先将 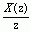展开成部分分式，然后再对每个分式乘以 （即写成X(z)的展开式）。这样，对于X(z)的一阶极点 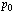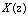， 含有一个 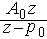形式的部分分式；而对于X(z)的s阶极点 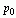，则含s个形如 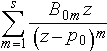的部分分式。至于这些部分分式各自的待定系数，则可以利用附录中介绍的方法来确定（当然，如果读者愿意，也可以用联立待定系数方程组来求解）。

　　这里要特别提请读者注意的一点是，由于所需要的z变换的基本形式为 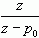，因此这里部分分式展开的对象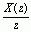是 ，而不是 。