4.5.10 z域卷积定理

　　已知两个序列x(n)和y(n)，它们的z变换分别为

 ,

 ,

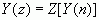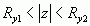
　　则这两个序列乘积序列的Z变换为

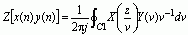
　　或

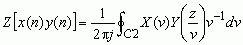
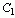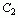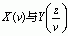　　其中 为 收敛域重叠部分内逆时针旋转的围线，而 为 收敛域重叠部分内逆时针旋转的围线。 的收敛域一般为 或 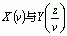的重叠部分，即 。

　　证明：由Z变换定义得

 (ZT定义)

 (IZT定义)

 (交换求和与积分的次序)

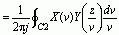 (ZT定义)

　　从上面的证明过程可以看出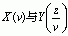， 的收敛域分别为

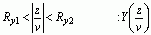
　　上两式相乘，从而可以得到Z[x(n)y(n)]的收敛域至少为

　　同理可以证明另一式，同学们可以自己证明。