4.5.8 终值定理

　　若 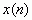是因果序列，且已知其z变换为

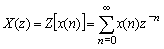
　　则

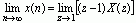
　　证明：因为

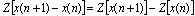 (线性性)

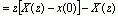 (时移性)

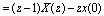
　　取极限可得

　　＝

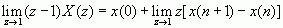
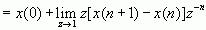
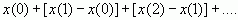
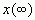　　= [证毕]

　　由证明过程可以看出，终值定理只有在 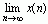存在时才可以应用,也就是说 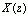的极点必须在单位圆内(如果位于单位圆上，则只能位于 点，且是一阶极点)。

　　下面我们举例来说明终值定理的应用条件。

　　例：设序列为 ，可求出其Z变换为 ，取极限可得 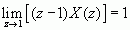。但显然序列的极限并不存在，即 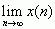不存在，所以

　　导致上面这种“终值定理”不成立的原因是X(z)在单位圆外有极点。

　　终值定理的应用类似于拉氏变换的终值定理，如果已知序列x(n)的z变换X(z)，在不求逆变换，且满足终值定理地应用条件时，就可以直接利用终值定理很方便地求出序列的终值