4.5.6 时域共轭

　　本性质表明序列求共轭后Z变换发生什么变化。

　　若已知

　　　　Z[x(n)]=X(z)

　　则

 ( )

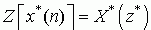　　直接根据ZT的定义是不难证明这一结论的，留给读者自己来证明。

　　特别地，如果序列是实序列，因为实数的共轭是它自己，所以此时有下面的等式成立

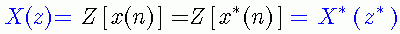
　　这样，我们就又可以得到与上一小节类似的结论：

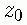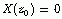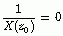　　若实序列有一个零点（极点） ，也就是说 （ ）成立，那么根据这里的的结论，它一定也会有 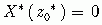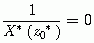（ ）成立，即 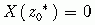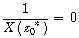（ ）成立，也就是说 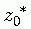也是X(z)的一个零点（极点）。

4.5.7 初值定理

　　若 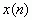是因果序列，且已知其z变换为

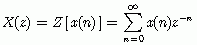
　　则

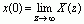 证明：由z变换的定义可得

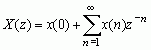
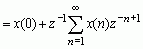
　　所以

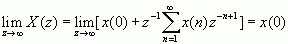
　　上式中除第一项x(0)外，其余各项当z趋于无穷大时，z^-1趋于零，所以因果序列的初值为

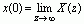
　　初值定理的应用类似于拉氏变换的初值定理，如果已知序列x(n)的z变换X(z)，在不求逆变换的情况下，就可以直接利用初值定理很方便地求出序列的初值。当然也可以用这条性质来验证所求Z变换式是否正确。如果所求出的初值与序列的真实初值不一致，则所求Z变换一定有问题；不过，即便是一致的，也不能肯定所求Z变换式是正确的。