4.5.5 序列反褶

　　此性质揭示的是当序列在时域发生反褶时，其Z变换结果会发生什么变化。

　　若已知

　　　　　　Z[x(n)]=X(z)

　　则

 ( )

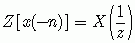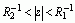　　证明：根据Z变换的定义式，得

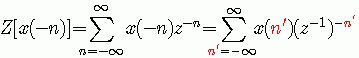
　　（请注意上面公式推导中的变量替换）

　　按照Z变换的定义，上式可写成

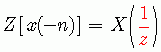
　　有了这一条性质，我们可以得到两个结论。

　　(a) 如果序列是一个偶对称序列，即 ，那么利用上述Z变换关于时间反褶序列的性质，可以得到下面的关系式成立：

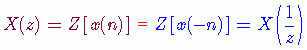
　　(b) 如果序列是一个奇对称序列，即 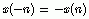，那么它的z变换满足

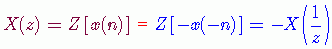
　　从上面所得的关于对称序列的两个结论，我们不难看出，如果一个对称序列（不论它是偶对称序列，还是奇对称序列）有一个零点（极点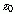） ，也就是说 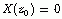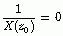（ ）成立，那么根据上面的结论，一定也会有 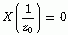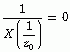（ ）是成立的，而这个等式说明 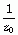也是X(z)的一个零点（极点）。