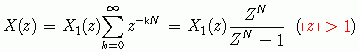下面我们来看看在单边Z变换的情况下，序列发生时移后，收敛域的变化。

　　（2） 单边z变换

　　　若x(n)为双边序列，其单边z变换为

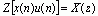
　　　则序列左移后，它的单边z变换为

 （ ）

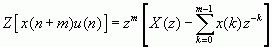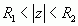　　证明：根据单边z变换的定义，可得

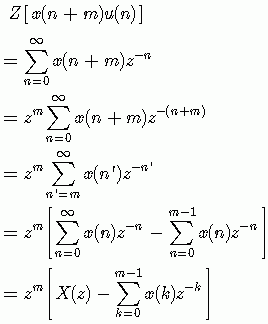
　　同样，可以得到右移序列的单边z变换

 （ ）

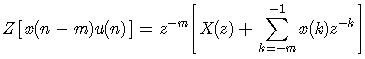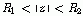　　其中m为任意正整数

　　如果x(n)是因果序列，由于当n<0时 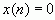，则上式中的 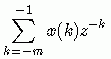项都等于零。所以右移序列的单边z变换为

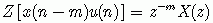
　　显然，如果进行右移的序列原来是因果序列，则所得的新序列的单边z变换与双边z变换相同。为什么？因为序列如果是因果序列的话，则它在负轴方向取值为零，右移后新序列在负轴方向的取值仍然是零，所以对双边Z变换而言，在负轴方向序列对Z变换式没有“贡献”，即因果序列的单边Z变换与双边Z变换是相同的。

　　下面我们来看一个例子。

　　例：已知序列为

　　它的Z变换为

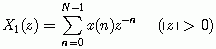
　　若将此序列以周期N进行周期延拓（即周期重复），可得周期序列（周期为N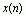） 。试求周期序列 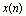的单边z变换。

　　　解：根据周期延拓的方法，可以将周期序列x(n)表示为下面的形式

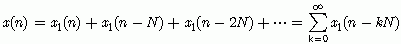
　　结合序列Z变换的线性特性与时移特性，我们可以得到