4.3.5 Z变换零极点与收敛域的关系

　　序列的ZT存在零点和极点。这是因为序列的ZT同信号的LT一样都是复变函数，区别只是自变量名称不同，因此其零点和极点的定义与LT的零点与极点的定义相同。在z平面上，用“”表示零点位置，“×”表示极点位置。

　　关于极点与ROC的关系，我们有以下一些结论。

　　结论1：通常情况下，序列的ZT在其ROC内是解析的，因此ROC是一个以极点为边界的、不含任何极点的连通域。

　　记住这一条结论，对理解后面的三条结论很有帮助。ROC的特点(或要求)是：

　　(1) 以极点为边界；(2) 不含任何极点（内部没有洞）；(3) 本身是连通的。

　　结论2：右边序列ZT的ROC，是某圆外面的区域(不包括圆周)，且模最大的有限极点在该圆周上。

　　因为要求ROC是圆外部分――这是右边序列提出的要求。因为右边序列要求序列下标n的取值要到正无穷（右~~~边~~~序列嘛），所以z的取值就不能为零了！而零点即是圆心，因此圆的内部不可能是ROC（为什么？因为若是的话，就要在ROC内挖洞了，这不符合ROC的“精神”啊），ROC只能是圆外的部分。再者，正是因为n可以取正无穷，所以z也可以取正无穷，所以ROC也只能是圆外部分。所以不管是考虑零点，还是考虑z取值无穷大，都要求ROC是圆外的部分――所以圆边界上的极点是模最大的极点。

　　想想看，此时的ROC比最大的极点还要“大”(指在该极点的外面)，也只有这样才能保证所有的极点都不在ROC内!

　　结论3：左边序列ZT的ROC，是某圆内部的区域(不包括圆周)，且模最小的非零极点在该圆周上。

　　同理，因为要求ROC是圆内的部分――这也是左边序列提出的要求。（思路与前面讨论右边序列时相同）由于是左边序列，所以n的取值可以是负无穷大，因此z=0可以使序列ZT收敛，这说明Z平面的零点应在ROC内，即圆心在ROC内。再者，在n为负无穷时，为保证ZT收敛，z不能取无穷大（否则ZT式的分母就为零了――想想看，这是为什么？），因此圆外部分不能是ROC。综上述，对左边序列而言，ROC只能是圆内部分――所以圆边界上的极点是模最小的非零极点，惟其如此，才能让所有的极点都不在ROC内!

　　结论4：双边序列ZT的ROC，是某圆环区域(不包括两个圆周)，且模大小邻近的两极点分别在两圆周上。

　　要注意的是：这里只是说两圆周是用模大小相邻的两极点来确定的，并没有要求极点是模最大的一对，还是最小的一对。什么意思？我们看下面的一个例子，大家就明白了。

　　例4-2：设 ， 和 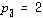是某一序列Z变换的三个极点，试指出序列Z变换各种可能的ROC。

　　解：根据前面的结论，该序列Z变换的ROC有以下4种可能：

　　(1) 以最小的模为半径的圆的内部区域，即：ROC为 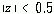，这是以0.5为半径的圆内部区域，这时序列为左边序列。

　　(2) 以大小相邻的模为半径的圆环内部区域，即：

　　(2.1) ROC为 ，即以0.5和1分别为内圆半径和外圆半径的圆环区域，这时的序列为双边序列。

　　(2.2) ROC为 ，即以1和2分别为内圆半径和外圆半径的圆环区域，这时的序列也是双边序列。

(3) 以最大的模为半径的圆的外面的区域，即：ROC为 ，这是以2为半径的圆外面的区域，这时序列为右边序列。

　　上面各种情况如图4-4所示。

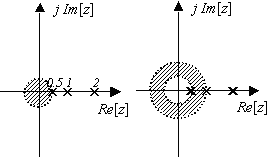
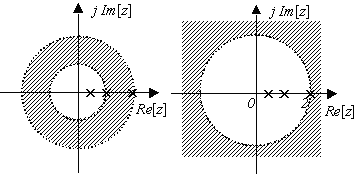
图4-4 序列Z变换可能的ROC形式