4.3.4 双边序列

　　如果序列在整个区间都有定义，则称之为双边序列，这是由于x(n)的n分布在原点的两边，故得名。利用前面所学的右边序列与左边序列的有关结论，可以先将双边序列分解成一个右边序列和一个左边序列的和的形式。这样，双边序列的z变换就可以写成下面的形式：

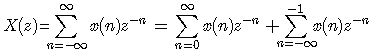_(4.21)

　　利用前面已得的结果，式 中第一项为右边序列，相应的收敛域为

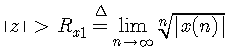_(4.22)

　　第二项为左边序列，相应的收敛域为

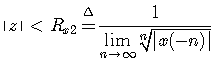_(4.23)

　　若 ，则双边序列z变换的ROC为上述两收敛域的重叠部分，即

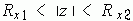
　　于是双边序列z变换收敛域是一个环形区域，如图4-3所示。

　　若 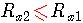，则上述两个序列的收敛域的交集为空，也就是说没有z能使级数收敛！即相应的双边序列不存在ZT。

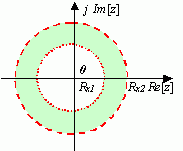
图4-3 双边序列的ROC （图中阴影部分）

　　最后要特别说明的是：

　　（1） 双边序列是所有序列的一般形式，其他序列都可以看成是双边序列的一种特例。（例如：右边序列是指n大于n₁时具有非零值的双边序列；左边序列是指n小于n₂时具有非零值的双边序列；而有限长度序列则是具有有限个非零值的双边序列。）因而，双边序列z变换的环状收敛域也是收敛域的一般形式，其他序列z变换的收敛域形式则是环状收敛域的一种特例。

　　（2） 由上述收敛域求法所得到的只是级数收敛的充分而非必要条件，级数的实际收敛域可能会更大。