4.3.3 左边序列

　　有右边，就有左边，所以下面我们来看看左边序列的Z变换收敛域的特点。先来看看什么是左边序列。

　　若序列 仅在 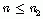时才取非零值，则称之为左边序列。这是一种无始有终的序列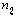， 是序列的终点。特别的，如果 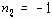（注意，－1是最大的负整数！），则序列称为反因果序列。

　　左边序列的ZT为

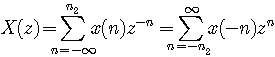_{( 4.18)}

　　注意，式(4.18) 中进行了变量替换，以便使用根值判别法求收敛域。

　　根据根值法，若

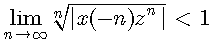　　　　( 4.19)

　　即

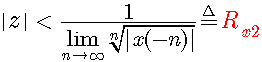　　　　( 4.20)

时，级数收敛。由此可见，左边序列z变换的收敛域是在z平面半径为 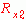的圆的内部。从前面的讨论我们已经知道，z平面的零点（原点）是一个特殊的点，那么左边序列的ROC是否含有零点呢？这要由序列终点的正负情况来决定。

　　（1）

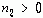
　　这时，左边序列的ROC为： 。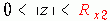

　　因为下标中有一部分正值，所以Z变换式中会含有z的负幂次项，当变量z=0时会导致这些项成为无穷大，因此其收敛域不能包括零点z=0。

　　（2）

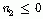
　　这时，左边序列的ROC为： 。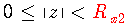

　　这时，所有的下标项都是非正的，因此Z变换式中都是z的正幂次项（可能还有一个零次幂），因而变量z可以等于零，也即序列的收敛域可以包括零点z=0。

　　下面是左边序列的收敛域示意图。

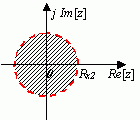
图4-2 左边序列的ROC（图中阴影部分）