4.3.2 右边序列

　　实际应用中所碰到的信号都可以视为因果信号（序列），这些序列的起点是时间零点，它们仅在零点（起点）的右边取非零值，是一种右边序列。下面我们来看一看任意起点的右边序列的收敛域情况。

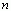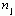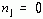　　如果序列 在 坐标轴上自 向右均有非零值，则称之为右边序列， 是序列的起点。特别地，若起点 ，则序列称为因果序列。显然，右边序列是一个有始无终的序列，其Z变换为

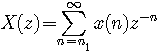
根据根值法，若

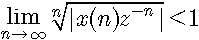
　　即

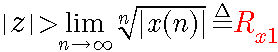
则该级数收敛。由此可见，右边序列z变换的收敛域是z平面上半径为 的圆的外部。

　　显然，无穷远点 是处于圆的外部的，那么它是否能被包含在收敛域内呢？需要满足什么条件吗？下面我们来讨论这些问题。

　　无穷远点是否能被包含在收敛域中，要视序列起点 的正负情况来定。具体来讲就是：

　　（1）

　　这时，右边序列的ROC为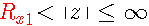： 。注意：这里的收敛域包含了无穷点。

　　这是由于n都是非负值，从而Z变换式中仅包含z的负幂次项，这样z就可以取无穷大值，即收敛域包括无穷远点。

　　（2）

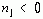
　　这时，右边序列的ROC为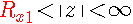： 。注意：这里的收敛域就不再能包含无穷远点了。

　　这是因为，当n可以取一部分负值时，Z变换式中会出现z的正幂次项，所以z就不能取无穷大，也即收敛域不能包括无穷远点。

　　下面是右边序列收敛域的示意图。

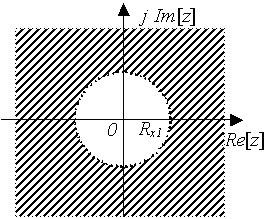
图4-1 右边序列的收敛域ROC (图中阴影区域)