(2) ROC内不会包含任何极点。

　　这是因为X(z)在极点处，其值将无穷大，Z变换不收敛，故收敛域不会包含极点，而且常常以X(z)的极点作为收敛域的边界。

　　(3) 在ROC内，ZT及其导数是z的连续函数，即ZT函数是收敛域内每一点的解析函数。

　　解析: 若复变函数在区域D内处处可微(可导)，在称其在区域D内是“解析”的。复变函数在某点解析，是指在它该点的邻域内是解析的。

　　好了，我们已经知道了ROC对于Z变换的重要意义，那么，如何来求解Z变换的ROC呢？

　　下面我们先来看看收敛域的一般求法，然后再讨论不同序列的Z变换ROC的特点。

　　由级数理论， 收敛的充要条件是它绝对可和，即

_(4.12)

　　而对于正项级数，可以用比值法和根值法来判别级数的收敛性。

　　对于正项级数求和 ，我们有下面两种方法判断该级数是否收敛：

　　(1) 比值法：

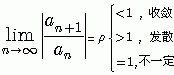_(4.13)

　　(2) 根值法：

_(4.14)

　　有了上面这两种方法，我们就可以求解一般序列的Z变换收敛域了。

　　下面我们根据上述判定方法进一步讨论不同序列Z变换的ROC。