从Z变换的定义式 可以看出，它是一种幂级数求和的形式。显然，这种幂级数和并不是总能收敛。这个式子既不是对所有的序列都能成立的，而且也不是对某序列的所有z值都成立。如果给定了具体的序列 ，则使其Z变换收敛的所有z值集合，称为X(z)的收敛域(ROC)。

　　上面给出了Z变换收敛域的定义。不过，这只是定义ROC的理由之一。必须引入ROC还有另外一个重要原因。在讨论这个重要原因之前，我们先来看看下面的一个例子。

　　这种说法是不是有点“似曾相识”啊？对的，在前面我们学习信号的拉氏变换时，关于为什么要定义拉氏变换的收敛域，我们也是提出了两条理由。现在讨论Z变换的收敛域，其理由也是相似的。

　　例4-1：根据上面关于Z变换收敛域的定义，试指出下列序列的收敛域。

　　　(1)

　　　(2)

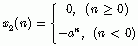
　　解：根据高等数学关于等比级数的求和方法，可求得序列 的ZT为

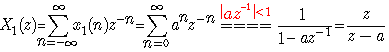
　　显然，要让上面的式子成立，可以求出它的ROC为 ；

　　同理，按照Z变换的定义，可以求得序列 的ZT为

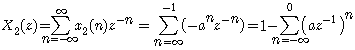
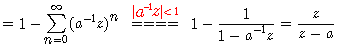
　　其中收敛域为 。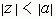

　　由例4-1我们可以看出，两个不同的序列(4.7)和(4.8)，却有着相同的Z变换结果，它们仅仅在ROC上有所不同!

　　这样一来，序列与Z变换结果之间就不是一一对应的了(如果去掉ROC信息的话)，我们也搞不清Z变换结果所对应的序列是什么了。那该怎么办呢？只有一种办法：即将ROC作为Z变换结果的不可或缺的组成部分。

　　由此可见，ROC对于序列的Z变换是非常重要的。因此，要描述一个序列的Z变换，必须包括两个部分：(1) Z变换的表达式X(z)；(2) Z变换的收敛域ROC。

　　另外，由例4-1我们还可以看出Z变换收敛域具有以下一般性的特点：

　　(1) Z变换收敛域的一般形式是z平面上以原点为中心的圆环，其表达式为

_(4.11)

　　这是因为，在 和 取特定值时，ROC可以从圆环变成其它形状。大家想想看，可能会有些什么形状？