(1) > 0 (即LT的收敛域在s平面右半边)

　　首先，收敛域没有将虚轴j 包含在内，所以傅里叶变换是不存在的，当然也就无所谓“用LT求FT”的讨论了。

　　其次，在这种情况下，衰减因子真的是起到衰减作用的，正是这种作用才将一些增长函数衰减下去，从而使新信号(经过衰减的乘积信号)存在傅里叶变换(实际上是原信号的拉氏变换)，如果不进行这样的衰减，即直接对原信号进行傅里叶变换，则信号显然是不能满足绝对可积的条件的，因此，在这种情况下，信号的傅氏变换是不存在的，当然同样也就无所谓“用LT求FT”的讨论了。

　　上面这两条理由都是用来说明此情况下不可能用前面的公式从LT求解FT。

　　(2) < 0 (即LT收敛域在s平面左半边)

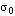　　 为负说明什么问题？意味着什么呢？

　　可以看出，对进行拉氏变换的信号，即使将它乘以增长因子(当 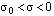时，信号在进行拉氏变换时所乘的所谓“衰减因子”实际已经变成了“增长因子”了!)，也能求出新信号的傅氏变换来，因此在不增长信号也不衰减信号(s=0，s=j)时---即原信号，信号的傅氏变换肯定也存在。因此，既然原信号的FT存在，就可以用上面的公式用LT来求解FT。

　　(3) 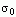= 0 (即LT收敛域的边界为s平面的虚轴)

　　在这种情况下，信号的傅氏变换可能存在，但不能简单地将拉氏变换中的s代以j 来求信号的傅氏变换----因为这时信号的傅氏变换中将包含奇异函数项，而在拉氏变换中却没有奇异项存在。例如，对于单位阶跃函数u(t)有：

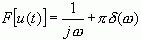
　　我们在信号的傅氏变换中发现了拉氏变换中无法对应的项。这些信息在拉氏变换中是不存在的，所以简单将自变量替换来求解傅氏变换是不行的。

　　下面导出收敛边界位于虚轴时拉氏变换与傅氏变换联系的一般关系式，若x(t)的拉氏变换为

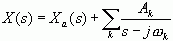
　　其中， 的极点位于s 平面之左半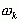， 为虚轴上的极点， 为部分分式分解的系数。容易求出上式对应的原信号为：

　　式中的 是对应 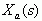之逆变换。求上式的傅氏变换可得

　　此处，“利用复指数信号的傅里叶变换结果”。

　　好了，上面我们分三种情况讨论了如何从信号的LT来求解其傅氏变换。通过学习，希望同学们能够建立起这样的观念：尽管傅里叶变换是拉氏变换的特例，但不能用自变量替换的方法来从拉氏变换求解傅氏变换。这里面，一是涉及到了增长信号无傅氏变换的问题，二是涉及到了傅氏变换中可能会出现奇异项的问题。大家一定要注意这个问题。