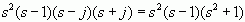由拉氏变换的定义式可知，欲求F(s)的逆变换可以按定义式进行复变函数积分求得。这个积分可以根据留数定理来计算。实际的拉氏变换式F(s) 经常可表示为s的有理分式，可借助部分分式分解法将F(s)表达式分解，分解后各项s函数式的逆变换可直接从常见函数拉氏变换表中查得，从而使拉氏逆变换的求解过程大大简化，不再需要进行积分运算了。

　　部分分式展开法',这里的部分分式分解也称部分分式展开，具体方法大家可以参见“有理分式的部分分式展开法”一节。

　　下面我们以例子来说明这种方法求解逆变换的过程。

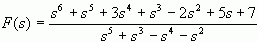　例3.5求 的原函数。为简便起见，不妨设原函数是因果函数。

　　　解：

　　　我们可以看出分式F(s)是一个假分式，先要化成真分式。

　　　 是一个假分式，将它改写为

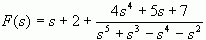
　　下面，我们先处理其中的真分式部分。

　　令

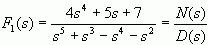
　　其中 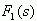为真分式。对 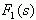的分母进行因式分解，得