3.4.1用留数定理求逆变换

　　留数定理为：在s平面沿一不通过被积分函数极点的封闭曲线C进行的围线积分等于此围线C中被积函数各极点p_i的留数之和，即

　　拉氏变换对中逆变换的定义式

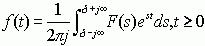
　　要利用留数定理求拉氏反变换，需要补充一条积分路线以构成一条积分围线C，所补充的积分路线为从积分限s - j¥至s + j¥的直线。如图3-1所示。

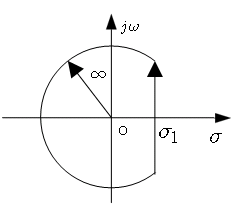
图3-1 F(s)的围线积分途径

　　于是，用留数定理求拉普拉斯逆变换的公式为：

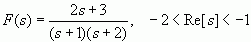　　例3.3 已知 。试用留数法求f(t)。

　　解：易见，F(s)的极点有两个s1=-1和s2=-2。它们对应的留数为

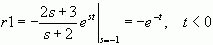
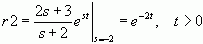
　　所以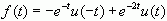

　　下面我们再看一个例子。

　　例3.4已知 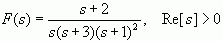。试用留数法求f(t)。

　　解：易见，F(s)的极点有三个s1=0, s2=-3, s3=-1，其中s3是二重极点。它们对应的留数分别为

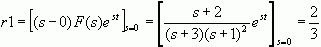
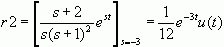
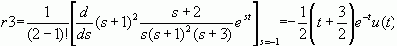
　　所以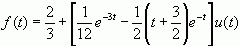

　　通过上面两个例子，我们可以看出：留数法的要点是求各极点所对应的留数。