上面是时域卷积定理，同理还可以得到频域卷积定理（也可称时域相乘定理）

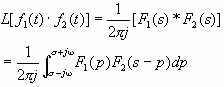
　　(10) 初值定理与终值定理

　　若信号 是因果信号，并且 及其导数 的拉氏变换存在，则可以从信号的拉氏变换结果求出信号的初值 和终值 ，方法如下：

　　需要说明的是：对于终值定理，须保证 存在才能使用。

　　当给定信号求其拉氏变换时，其初值和终值是知道的(可以直接计算出来)，因此，在求出信号的拉氏变换后，可以利用本性质对变换结果进行初步检验。即如果通过本性质(定理)求出的初值和终值与信号的实际初值或终值不一致，则说明在拉氏变换过程中出现了错误。但这种验证并不充分，因为当所求出的初值和终值与信号的真实情况相符合时，拉氏变换的结果仍有可能是错误的。

　　所以，同学们要注意，当算出的初值和终值与信号的实际值一致时，不要贸然简单地下结论，认为自己的拉氏变换结果没问题。真要这样(简单下了结论)，可能就真的出问题了。