(6) 时域积分　（可对照傅里叶变换性质中的时域积分、Z变换性质的时域积分、离散傅里叶变换性质的时域积分等内容。）

　　若 ，则

　　其中 是f(t)积分式在t=0的取值。

　　(7) 频域微分　（可对照傅里叶变换性质中的频域微分、Z变换性质的Z域微分、离散傅里叶变换性质的频域微分等内容。）

　　  若 ，则

　　(8) 频域积分　（可对照傅里叶变换性质中的频域积分、Z变换性质的Z域积分、离散傅里叶变换性质的频域积分等内容。）

　　   若 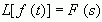，则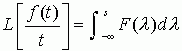

　　以上这些性质，比较容易理解，可以从拉氏变换的定义式直接进行推导。这里就不进行逐条证明了。

　　(9) 卷积定理　（可对照傅里叶变换性质中的卷积定理、Z变换性质的卷积定理、离散傅里叶变换性质的卷积定理等内容。）

　　若 ，

　　则

　　可见两个函数的卷积的拉氏变换等于两个函数的拉氏变换的乘积。