上面这些例子说明什么问题？

　　我们已经发现，例3.1与例3.2中的两个信号是不同的，但它们的拉氏变换结果却是一样的!不过，两个信号的拉氏变换能成立的条件(即LT的ROC)却是不相同的。这就说明，在给出一个信号的拉氏变换时，除了给出拉氏变换的表示式外，还不能不给出使表示式能够成立的复变量s的取值范围。反过来说，也只有给出了相应的ROC，拉氏变换才与特定的信号有对应关系。

　　值得指出的是，对于单边拉氏变换，由于其只能适用于因果信号，故其以收敛域位于收敛轴的右边，其形式比较简单。

　　现在，我们就明白了定义拉氏变换收敛域的必要性了。(1) 从定义出发，变换结果只在特定的域(ROC)内才能成立；(2) 从区分不同信号的相同变换结果出发，变换结果不能孤立存在，需要标明其存在的ROC才有意义。

　　好了，有了上述关于LT的定义，又进一步讨论和理解了拉氏变换ROC的概念及其必要性，我们在下一节来实际看看一些常见信号的拉氏变换。

3.2.3    常见函数的拉氏变换

(1)阶跃函数

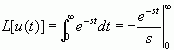
　　上式积分在Re[s]>0时收敛，故

　　同理，可求出-u(-t)的双边拉氏变换为：

　　可见，u(t)与-u(-t)具有相同的双边拉氏式，但它们的ROC却不相同。

(2)指数函数

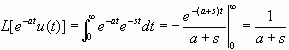        ,Re[s]>-a,其中a可正可负

(3) (n是正整数)

 ，  Re[s] > 0