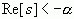3.2.2    拉氏变换的收敛域

　　前面我们在定义拉氏变换时说到：为了使一些增长信号能有傅里叶变换，我们引入了衰减因子，把这种增长“压下去”，从而使其(乘积信号)能进行傅里叶变换分析。这里有一个问题：如果压不下去怎么办？那不是连拉氏变换也不能应用了吗？回答是肯定的。压不下去的原因有两种：一是以现在这种形式的衰减因子，根本不可能使乘积信号衰减下来，如一些比指数函数增幅得更快的函数；二是衰减因子选择不适当-----如果衰减因子选得适当，拉氏变换还是存在的，这就涉及到下面我们要讲的LT的收敛域问题了。

　　从以上对LT定义的讨论可知，当函数f(t)乘以衰减因子 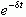以后，乘积信号就有可能满足绝对可积的条件，即存在傅里叶变换。然而，是否一定能够满足该条件，还要视信号f(t)的性质与s 值的相对关系而定。

　　这是什么意思啊？就是说，如果衰减因子没能把信号衰减下来，这个傅里叶变换就搞不成!所以衰减因子一定要名副其实，它的“功力”要够，“道行”要深。这就告诉我们：

　　需要选择适当的衰减因子，LT才有可能存在。例如，为使信号 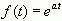收敛，衰减因子 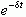中的s 必须满足s > a ，否则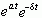， 在t-> 时仍不能收敛。

　　我们称使f(t)的LT存在的s的取值范围为LT的收敛域，简记为ROC。

　　这就告诉我们：是LT的定义要求我们要考虑LT的ROC。

　　下面我们先来看几个例子，然后再从另外一个角度来说明为什么要定义LT的ROC？即定义ROC的必要性是什么？

　　最开始我们所说的“使LT存在的要求”只是要定义LT的ROC的原因之一。

　　例3.1 试求信号 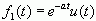的双边拉氏变换。

　　解：根据双边拉氏变换的定义，可求得信号的双边拉氏变换为

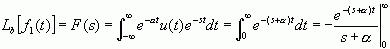
　　上述积分只有当 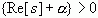，即 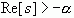时才收敛，于是

, 

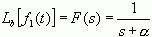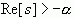
　　因此在本例中，拉氏变换仅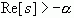在 时存在。

　　如果a为正，那么F(s)就能在 = 0处求值，即

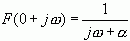
　　上式表示= 0时的拉氏变换，等于傅里叶变换；

　　如果a为负，拉氏变换仍存在，但傅里叶变换不存在。

　　为了对比，我们再看下面的一个例子。

　　例3.2 试求信号 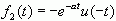的双边拉氏变换。

　　解：根据双边拉氏变换的定义，可求得信号的双边拉氏变换为

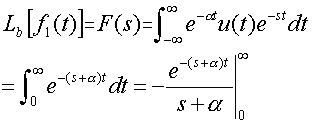
　　上述积分只有当 ，即 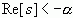时才收敛，于是

,
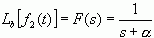