因此,式(1a)和(1b)可改写为:
![]() (2a)
(2a)
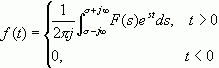 (2b)
(2b)
(2a)和(2b)式称为单边拉氏变换的一对变换式。其中(2a)式中积分下限取 ![]() 是考虑f(t)中可能包含冲激函数等奇异函数,但为了简便,常把下限写为0,只有必要时才把它写为
是考虑f(t)中可能包含冲激函数等奇异函数,但为了简便,常把下限写为0,只有必要时才把它写为
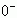 。同样,(2b)式中也常常只写t>0的部分。
。同样,(2b)式中也常常只写t>0的部分。
通常,以记号 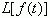 表示对f(t)取单边拉氏变换,记为
表示对f(t)取单边拉氏变换,记为
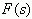 ,以
,以 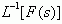 表示对
表示对 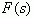 取单边拉氏逆变换,于是
取单边拉氏逆变换,于是
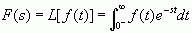 (3a)
(3a)
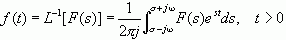 (3b)
(3b)
上式就是目前应用得比较广泛的单边拉氏变换的一对表达式。单边拉氏变换对于分析具有初始条件的线性常系数微分方程描述的因果系统具有重要意义。
本课程主要讨论单边拉氏变换,对双边拉氏变换在讨论时将特别注明。对于因果信号,由于t<0时f(t)=0,故其双边拉氏变换与单边变换是相同的。正因如此,再加上因果信号是实际能碰到的信号,所以单边拉氏变换应用广泛。
今后若不作特别说明,都是指单边拉氏变换。
LT变换结果的自变量s是复数,与FT相对应,我们称之s为复频率,相应的所有取值构成的集合称为复频域,或称s域。
由于象函数是自变量为复数的函数,因此是复变函数,而我们以前过的自变量是实数的函数则是实变函数。
因此,LT方法是一种复频域变换方法,常被称为S域分析。
在上面的讨论中,我们将衰减因子引入傅氏变换,从而推得拉氏变换。从数学方法上看:将函数f(t)乘以衰减因子使之变为收敛函数,满足绝对可积条件;而从物理意义上看:将频率![]() 变换为复频率S,
变换为复频率S,![]() 只能表示振荡的重复频率,而s不仅能给出重复频率,还可以表达振荡幅度的增长或衰减速率。
只能表示振荡的重复频率,而s不仅能给出重复频率,还可以表达振荡幅度的增长或衰减速率。