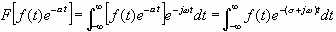3.2.1    从傅里叶变换到拉普拉斯变换

　　为什么要引入拉普拉斯变换呢？

　　经过前面一章的学习，我们知道，当函数f(t)满足狄义赫利条件时，便有下面的傅里叶变换对成立：

　　由前面的章节可知，在用频域法分析系统时，常需要求出信号f(t)的傅里叶变换，即信号f(t)的频谱为

　　然而，有不少信号函数不能直接由上面的定义求得其傅里叶变换。这通常是由于，当t趋向无穷大时，f(t)的幅度不衰减，因而积分不收敛的缘故。例如，单位阶跃函数u(t)，其傅里叶变换存在，但上式表示的积分不收敛。此外，由于傅里叶变换中绝对可积(狄义赫利条件)要求的限制，有些信号根本就不存在傅里叶变换。比如，一些随时间而不断增强的信号，如t随时间增幅的指数函数 的傅里叶变换就不存在。

　　这就是说，有的信号，傅里叶变换是存在的，但是无法用上面的定义式来求；而有些信号的傅里叶变换根本就不存在，更谈不上用上面的定义式来求了。

　　从另一方面讲，某些信号虽可进行傅里叶变换，但是其变换结果中出现了冲激函数。例如在阶跃信号、周期信号等信号的傅里叶变换结果，就要借助于冲激信号来表达。这样有时很不方便。

　　而冲激函数是一种奇异信号，它是为了研究方便而引入的抽象的数学概念，没有实际的物理信号对应。所以在变换结果中出现这类信号，总是有些不直观。

　　那怎么解决这些问题呢？

　　为了使对信号的分析过程更方便，简化运算形式及运算过程，也为了对不能进行傅里叶变换的信号进行变换分析，使更多的信号函数存在变换，我们引入一个衰减因子 (其中 为任意常数),将其与信号f(t)相乘，选取合适的实数，使乘积信号满足绝对可积条件(即狄义赫利条件)，从而能够进行下面的傅里叶变换：