在前面一章里，我们学习了连续时间信号的傅立叶变换。在涉及信号和线性时不变系统的众多领域里，傅氏变换都是非常有用的，在很大程度上这要归功于许多信号都能用复指数信号的线性组合来表示。用
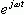的复指数信号的线性组合来表示连续时间信号，这是傅立叶分析和变换的基础。
在傅里叶变换里，复指数函数的指数为j
t，它只能随时间在虚轴j上变化，如果将其变化的范围扩展到整个复数平面，那又如何呢？
如果进一步将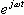 
扩展为复变量S（S=
+j）的复指数函数，也就是说把连续信号看作是无穷多项
之叠加，我们会得到更多的好处。什么好处？我们后面会提到。这就由傅里叶变换推广至拉普拉斯变换，简称拉氏变换。
因此，我们可以把拉氏变换理解为是傅立叶变换的推广，而把傅立叶变换看作是拉氏变换取在s=j
时的一种特例
这种变换方法的确立经过了一段过程。十九世纪末，英国工程师亥维赛德(O. Heaviside, 1850~1925)发明了算子法，很好地解决了电力工程计算中遇到的一些基本问题，但缺乏严密的数学论证。后来，法国数学家拉普拉斯(P. S. Laplace，1749~1825)在著作中对这种方法给予严密的数学定义。于是这种方法便被取名为拉普拉斯变换，简称拉氏变换。----因为是“拉普拉斯”这个人定义的。
拉普拉斯变换的变换域是复频率域。拉普拉斯变换方法是对连续时间系统进行分析的重要方法之一，同时也是其他一些新变换方法的基础。它在电学、力学等众多科学与工程领域中得到了广泛应用。
在20世纪70年代以后，计算机辅助设计(CAD)技术迅速发展，人们借助于CAD程序(如SPICE程序)，可以很方便地求解电路分析问题，这样就导致拉氏变换在这方面的应用相对减少了。此外，随着技术的发展和实际的需要，离散的、非线性的、时变的等类型系统的研究与应用日益广泛，而拉氏变换在这些方面却无能为力，于是，它长期占据的传统重要地位正让位给一些新的方法。
然而尽管如此，利用拉氏变换建立的关于系统函数及其零极点分析的概念仍有重要的意义，还在发挥着重要的作用。同时，在连续、线性、时不变系统的分析中，拉氏变换至今仍是不可缺少的强有力工具。最后，我们还应注意到与拉氏变换类似的概念和方法在离散时间系统的Z变换分析中得到的应用。这真是“灵魂不死，思想永在”啊。
本课程考虑到计算机作为工具日益得到广泛的应用，离散系统和数字信号处理的应用领域也不断扩大，所以对于拉普拉斯变换这部分内容，我们只作比较简要的介绍，不作很深入的讨论。