我们常常遇到需要将连续信号变为离散信号的情况，这就需要对信号进行抽样，或称取样或采样。例如，由于数字计算机无法直接处理模拟信号，因此需要在处理之前将模拟信号变成数字信号。这包含两个部分：(1) 信号取值时间离散化，即只保留信号在等间隔时间点处的取值；(2) 信号样值幅度离散化，即只用固定比特位数的整数来表示信号样值。处理后的信号将是数字化了的均匀抽样序列。

　　问题是：（1）抽样信号的傅里叶变换是什么样子？它与未经抽样的原信号的傅里叶变换有什么关系？
　　　　　　（2）信号的离散化（信号被抽样）是否会引起信息丢失呢？换句话说就是，能否由离散的信号（抽样信号）无失真地恢复出原始连续信号？如果能，离散化是否还需要满足什么条件？
对这些问题，本节将予以详细讨论。

2.9.1 抽样信号的FT

　　抽样过程可以理解为利用抽样脉冲序列P(t)从连续信号f(t)中抽取一序列离散样值的过程，这样得到的信号通常称为抽样信号，常记作fs(t)。上述抽样过程是在时域进行的，称为时域抽样。

　　大家要注意，在信号处理领域中，习惯上把Sa(t)称为"抽样函数"，它与这里所讲的"抽样"或"抽样信号"有完全不同的含义。

　　下面我们以冲激抽样（理想抽样）为例，来说明抽样信号的傅里叶变换与原连续信号的傅里叶变换之间的联系。

　　最简单的抽样过程是以冲激序列T(t)当抽样序列P(t)，称为自然抽样或冲激串抽样，也被称为理想抽样。抽样过程的数学表示为

　　　　　　　　　　(2-49)

　　由频域卷积定理，抽样信号的FT为

　　　　　

　　　　　代入周期冲激序列的FT

　　　　　

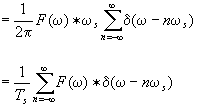
　　　　　利用冲激函数的搬移特性

　　　　　　　　（2-50）

　　信号经理想抽样前后的频谱变化情况见图2-14(abc或abd)。

　　
　　
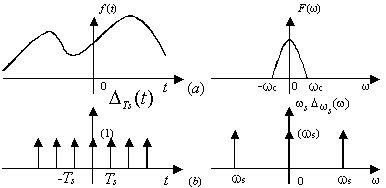
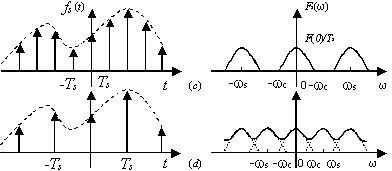
　　　　　　　　　　图2-14 信号理想抽样的FT

　　式(2-50)告诉我们：理想抽样信号的频谱函数是原信号频谱函数的1/Ts按周期s (s=2/Ts)进行周期延拓的结果，因此是一个周期函数。