(2) _T(t)的FT频谱由式(2-41)可得

　　　　　(2-45)

　　式中₁=2/T₁。上式表明，周期单位冲激序列的频谱只包含n₁(n=0, ±1, ±2, …)频率处的冲激函数，其强度均等于₁。

　　前面我们探讨了周期信号的傅里叶级数与傅里叶变换的关系，还探讨了周期信号的傅里叶级数与其主周期内信号的傅里叶变换的关系，下面我们来看看周期信号的傅里叶变换与其主周期内信号的傅里叶变换之间的关系。

　　设周期为T₁的周期信号f(t)在主周期内的函数为f₀(t)，如果不断将f0(t)平移到信号f(t)的其它各个周期处，则可以得到整个周期信号f(t)。这样，f(t)可表示为

　　　　　　　(2-46)

　　如何进行上述的平移操作呢？记得我们以前介绍的冲激函数的搬移特性吗？通过与冲激信号相卷积，可以将信号"搬移"到冲激信号的冲激点。

　　上面的结果可以用冲激序列与信号f₀(t)的卷积来实现，即

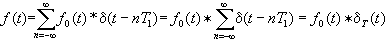　(2-47)

　　f₀(t)是非周期信号，其FT一般是存在的，不妨设其为F₀()。根据FT的卷积定理，周期函数f(t)的FT可以用F₀()与冲激序列_T(t)的FT相乘得到。而冲激序列的FT在前面的例2-8中已经求出来了，为

　　　

　　有了冲激序列的FT，对式(2-47)利用卷积定理可得

　　　(2-48)

　　由式(2-48)，我们可以得出结论：

　　周期为T₁的周期信号f(t)的傅里叶变换F()，是一个离散间隔为₁的冲激序列，其中在频率处的冲激的强度，等于该信号在第一个周期内函数f₀(t)的傅里叶变换F₀()在该频率处抽样值F0(n₁)的₁倍。