利用傅里叶级数FS，我们可以对周期信号进行频谱分析；之后我们通过让周期趋于无穷大的方法的引出了傅里叶变换(FT)，解决了对非周期信号进行频谱分析的问题。现在，我们自然要问，那对周期信号能否使用FT进行频谱分析呢？如果能的话，我们将能用傅里叶变换来统一对所有信号（周期的和非周期的）进行频谱分析了（如果信号存在FT的话）。

　　在讨论一般周期信号的FT之前，我们先来看看一些特殊周期信号的FT。

2.8.1 正余弦信号的FT

　　由直流信号的FT结果及FT的频移性质，

　　　

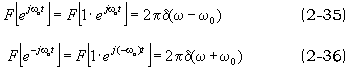
　　将上面两个式子分别相加、相减，并利用欧拉方程，

　(2-37)

　　　　　　　　(2-38)

　　结果见图2-4。

　　　　
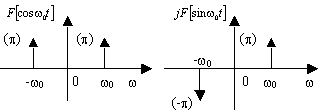
　　　　　　　图2-4 余弦函数和正弦函数的FT

下面我们对上图作一个直观的解释：
　　（1）由于正弦和余弦信号都是单一频率的信号，而傅里叶分析是将信号分解为三角函数的加权和形式，因此正弦和余弦信号仅在其频率w0处才有分量。
　　（2）信号能量是有限的，但其频域只有一点，根据能量守恒（帕斯瓦尔定理），该点的频谱密度将无穷大，这种频谱只能用冲激函数来刻划。
　　（3）考虑到FT是FS的推广，它把每个频率处的频率分量都"一分为二"地放置在正负频率处。