2.7.13 频域卷积定理

　　与时域卷积定理类似，

　　证明方法同时域卷积定理，在这里不在重复，同学们可自己证明。

　　由上可见，两个时间函数频谱的卷积等效于两个时间函数的乘积。或者说，两个时间函数乘积的频谱等于各个函数频谱乘积乘以1/2。

　　显然，时域与频域卷积定理是对称的，这是由傅里叶变换的对称性决定的。

2.7.14　帕斯瓦尔定理

　　前面我们在讲信号分解时，提及帕斯瓦尔定理。下面我们来研究一下该定理在FT中的具体表现形式。

　　若F[f(t)]=F() ，则

　　　　　　

　　这就是帕斯瓦尔定理在傅里叶变换中体现，它表明了信号的能量在时域与频域是守恒的。下面利用FT的定义和性质，推导信号能量的求解。
　

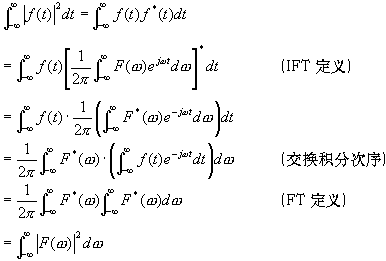
　　式中 是信号f(t)的总能量， |F()|²为信号f(t)的能量谱密度。

　　帕斯瓦尔定理表明，这个总能量既可以按每单位时间的能量|f(t)|²在整个时间内积分计算出来，也可以按单位频率内的能量|F()|²/2在整个频率范围内积分来得到。

　　此定理也可以如下证明。由相关性定理可得

　　　　　

　　取t=0，即得帕斯瓦尔定理。