2.7.10 时域积分

　　若F[f(t)]=f() ，则
　　
　　证明：
　　　　　

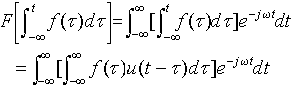
　　变换积分次序，并且利用阶跃信号的傅里叶变换关系式

　　　　　　
　　于是
　　　　

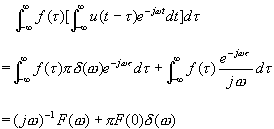
　　特别地，如果 处有界，则

　　　　

　　例2.7 利用时域积分特性求F[u(t)] 。

　　解：由于F[(t)]=1 ，且
　　　　　　　　　　　　　　
　　由时域积分特性可得
　　　　　　　　　　　　
　　可见，这与利用符号函数求得的结果一致。

2.7.11 频域积分

　　若F[f(t)]=F() ，则有

　　

2.7.12 时域卷积定理

　　
　　证明：


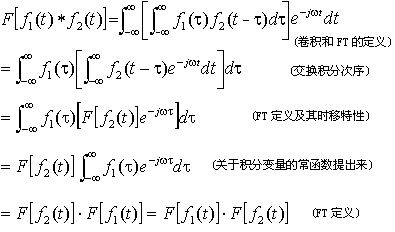
　　由上可见，两个时间函数卷积的频谱等于各个时间函数频谱的乘积，也就是说，两信号时域卷积等效于频谱相乘。