由上可以看出，信号f(t)在时域中沿时间轴右移（延时）t₀等效于在频域中频谱乘以因子，也就是说，信号右移后，其幅度谱不变，而其相位谱却产生了附加相位变化（-t₀），各频谱分量的相位落后t₀。同理，若信号f(t)在时域中沿时间轴左移（超前）t₀等效于在频域中频谱乘以因子 ，这时，其相位谱也产生了附加相位变化（t₀），各频谱分量的相位超前wt₀。

2.7.7　频移

　
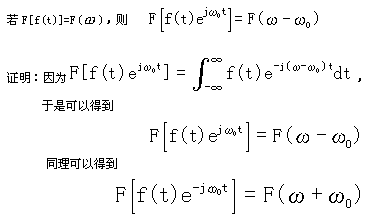
　　 　　由上可见，若信号f(t)乘以因子，等效于f(t)的频谱F()沿频率轴右移₀。也就是说，在频域中将频谱沿频率轴右移₀等效于在时域中信号乘以因子。同样，若信号f(t)乘以因子，等效于f(t)的频谱F()沿频率轴左移₀。

　　例2.5　已知f(t)=cos(₀),利用频移定理求余弦信号的频谱。

　　　　　　解：因为F[1]=2() ，则由频移定理得

　　　　　　　　

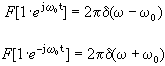
　　利用欧拉公式和FT的线性，可得

　　　　　

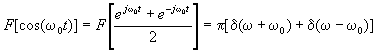
　　同理可得sin(₀t)的傅里叶变换，请同学们自己试着做做看。