2.7.5 尺度变换

　　若F[f(t)]=F()，则
　　　　　　　　　　　　　　
　　这里a是非零的实常数。

　　下面利用FT的定义及积分的性质，分a>0和a<0两种情形来证明傅里叶变换的尺度变换特性。

　　证明：因为
　　　　　　　　　　
　　令at=x，

　　当a > 0时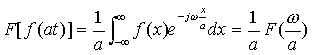 　

　　当a < 0时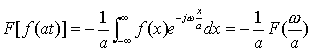　

　　上述两种情况可综合成如下表达式：

　　　　　　　　　　　

　　由上可见，若信号f(t)在时域上压缩到原来的1/a倍，则其频谱在频域上将展宽a倍，同时其幅度减小到原来的1/a。

　　尺度变换性质表明，在时域中信号的压缩对应于频域中信号频带的扩展，反之，信号的时域扩展对应于频域的压缩。对于a=-1的特殊情况，它说明信号在时域中沿纵轴反褶等效于在频域中频谱也沿纵轴反褶。

　　对傅里叶变换的尺度变换特性最通俗的解释可以采用生活中的实例来说明，在录音带快放时，其放音速度比原磁带的录制速度要快，这就相当于信号在时间上受到了压缩，于是其频谱就扩展，因而听起来就会感觉到声音发尖，即频率提高了。反之，当慢放时，放音的速度比原来速度要慢，听起来就会感觉到声音浑厚，即低频比原来丰富了（频域压缩）。

2.7.6 时间平移(延时)

　　

　　下面进行证明

　　证明：

　　
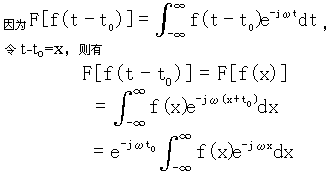
上式右边的积分项为傅里叶变换定义式，

　　于是可以得到
　　　　　　　　　　　　
　　同理可以得到