2.7.4对称性

　　傅里叶变换与傅里叶反变换之间存在着对称关系，称为傅里叶变换的对称性质。若已知

　　　　　F()=F[f(t)]
则有
　　　　　F[f(t)]=2f(-)

　　证明：因为
　　　　　　　　
　　于是
　　　　　　　　

　　将变量t与互换，再将2乘过来，得
　　　　　　　　
　　上式右边是傅里叶正变换定义式，被变换函数是F(t)

　　所以
　　　　　　　　F[F(t)]=2f(-)

　　若f(t)为偶信号，即f(t)=f(-t)，则有
　　　　　　　　F[F(t)]=2f()

　　从上式可以看出，当f(t)为偶信号时，频域和时域的对称性完全成立――即f(t)的频谱是F()，F(t)的频谱为f()。

　　若f(t)为奇信号，即f(t)=-f(-t)，则有
　　　　　　　　F[F(t)]=-2f()

　　利用FT的对称性，我们可以很方便地一些信号的傅里叶变换。下面我们举些例子来说明这一点。

　　例2.2 试根据FT的对称性，利用冲激信号的傅里叶变换来求直流信号的傅里叶变换。

　　解：已知冲激信号的傅里叶变换为F[E(t)]=E，将E视为常数函数，它是偶函数，根据FT的对称性，得F[E]=2E()。

　　例2.3 试根据FT的对称性，利用矩形脉冲信号的傅里叶变换来求解Sa函数的傅里叶变换。

　　解：已知矩形脉冲信号的傅里叶变换为
　　　　　　
　　根据FT的对称性，可得
　　　　　　　　　　　　
　　若令=2、E=1，则
　　　　　　　　　　　　
　　即Sa函数的FT是脉宽为2、脉高为p的矩形脉冲。矩形脉冲信号波形与频谱、Sa函数的波形与频谱如下图所示。

　　　
　
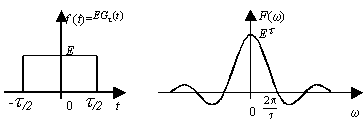
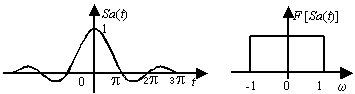
　　　　　　图2-12 根据FT的对称性求Sa函数的FT

　　例2.4 试根据FT的对称性，利用符号函数的傅里叶变换来求解求信号f(t)=1/t的傅里叶变换。

　　解：已知符号函数的傅里叶变换为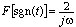，根据FT的线性可得
　　　　　
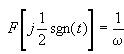
　　根据FT的对称性，考虑到sgn(t)是奇函数，有